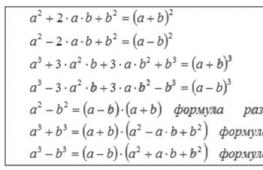How to put together a formula for reduced multiplication. Abbreviated Multiplication Formulas - Knowledge Hypermarket. Formulas for squares

02.12.2020

Abbreviated multiplication formulas.

Study of abbreviated multiplication formulas: the square of the sum and the square of the difference of two expressions; difference of squares of two expressions; sum cube and difference cube of two expressions; sum and difference of cubes of two expressions.

Application of abbreviated multiplication formulas when solving examples.

To simplify expressions, factorize polynomials, and bring polynomials to a standard form, abbreviated multiplication formulas are used. Abbreviated multiplication formulas need to be known by heart.

Let a, b R. Then:

1. The square of the sum of the two expressions is square of the first expression plus twice the product of the first expression by the second plus the square of the second expression.

(a + b) 2 \u003d a 2 + 2ab + b 2

2. The squared difference of the two expressions is square of the first expression minus twice the product of the first expression by the second plus the square of the second expression.

(a - b) 2 \u003d a 2 - 2ab + b 2

3. Difference of squarestwo expressions is equal to the product of the difference of these expressions and their sum.

a 2 - b 2 \u003d (a -b) (a + b)

4. Sum cubetwo expressions is equal to the cube of the first expression plus three times the square of the first expression and the second plus three times the first expression and the square of the second plus the cube of the second expression.

(a + b) 3 \u003d a 3 + 3a 2 b + 3ab 2 + b 3

5. Difference cubetwo expressions is equal to the cube of the first expression minus three times the square of the first expression by the second plus three times the product of the first expression and the square of the second minus the cube of the second expression.

(a - b) 3 \u003d a 3 - 3a 2 b + 3ab 2 - b 3

6. Sum of cubestwo expressions is equal to the product of the sum of the first and second expressions by the incomplete square of the difference of these expressions.

a 3 + b 3 \u003d (a + b) (a 2 - ab + b 2)

7. Difference cubes two expressions is equal to the product of the difference of the first and second expressions by the incomplete square of the sum of these expressions.

a 3 - b 3 \u003d (a - b) (a 2 + ab + b 2)

Application of abbreviated multiplication formulas when solving examples.

Example 1.

Calculate

a) Using the formula for the square of the sum of two expressions, we have

(40 + 1) 2 \u003d 40 2 + 2 40 1 + 1 2 \u003d 1600 + 80 + 1 \u003d 1681

b) Using the formula for the square of the difference of two expressions, we get

98 2 \u003d (100 - 2) 2 \u003d 100 2 - 2 100 2 + 2 2 \u003d 10000 - 400 + 4 \u003d 9604

Example 2.

Calculate

Using the formula for the difference between the squares of two expressions, we get

Example 3.

Simplify expression

(x - y) 2 + (x + y) 2

We will use the formulas for the square of the sum and the square of the difference of two expressions

(x - y) 2 + (x + y) 2 \u003d x 2 - 2xy + y 2 + x 2 + 2xy + y 2 \u003d 2x 2 + 2y 2

Abbreviated multiplication formulas in one table:

(a + b) 2 \u003d a 2 + 2ab + b 2
(a - b) 2 \u003d a 2 - 2ab + b 2
a 2 - b 2 \u003d (a - b) (a + b)
(a + b) 3 \u003d a 3 + 3a 2 b + 3ab 2 + b 3
(a - b) 3 \u003d a 3 - 3a 2 b + 3ab 2 - b 3
a 3 + b 3 \u003d (a + b) (a 2 - ab + b 2)
a 3 - b 3 \u003d (a - b) (a 2 + ab + b 2)

Mathematical expressions (formulas) abbreviated multiplication (the square of the sum and the difference, the cube of the sum and the difference, the difference of the squares, the sum and the difference of the cubes) are extremely irreplaceable in many areas of the exact sciences. These 7 symbolic notations are irreplaceable for simplifying expressions, solving equations, multiplying polynomials, canceling fractions, solving integrals and much more. This means that it will be very useful to understand how they are obtained, what they are for, and most importantly, how to remember them and then apply them. Then applying abbreviated multiplication formulas in practice, the most difficult thing will be to see what is xand what have. Obviously, there are no restrictions for a and bno, which means it can be any numeric or literal expressions.

And so they are:

The first x 2 - at 2 \u003d (x - y) (x + y) .To calculate difference of squares two expressions must be multiplied by the differences of these expressions by their sums.

The second (x + y) 2 \u003d x 2 + 2xy + y 2 ... To find squared sum two expressions, you need to add the double product of the first expression to the second plus the square of the second expression to the square of the first expression.

Third (x - y) 2 \u003d x 2 - 2xy + y 2... To calculate squared differencetwo expressions, you need to subtract the double product of the first expression by the second plus the square of the second expression from the square of the first expression.

Fourth (x + y) 3 \u003d x 3 + 3x 2 y + 3x 2 + y 3. To calculate cube sumtwo expressions, you need to add to the cube of the first expression the triple product of the square of the first expression by the second plus triple the product of the first expression by the square of the second plus the cube of the second expression.

The fifth (x - y) 3 \u003d x 3 - 3x 2 y + 3x 2 - at 3... To calculate difference cubetwo expressions, it is necessary to subtract from the cube of the first expression the triple product of the square of the first expression by the second plus triple the product of the first expression by the square of the second minus the cube of the second expression.

Sixth x 3 + at 3 \u003d (x + y) (x 2 - xy + y 2) To calculate sum of cubestwo expressions, you need to multiply the sums of the first and second expressions by the incomplete square of the difference between these expressions.

Seventh x 3 - at 3 \u003d (x - y) (x 2 + xy + y 2) To perform a calculation difference cubestwo expressions, the difference between the first and second expressions must be multiplied by the incomplete square of the sum of these expressions.

It is not difficult to remember that all formulas are applied to perform calculations in the opposite direction (from right to left).

The existence of these regularities was discovered about 4 thousand years ago. They were widely used by the inhabitants of ancient Babylon and Egypt. But in those times, they were expressed verbally or geometrically and did not use letters in the calculations.

Let's analyze sum square proof(a + b) 2 \u003d a 2 + 2ab + b 2.

The first this mathematical regularity proved by the ancient Greek scientist Euclid, who worked in Alexandria in the 3rd century BC, he used for this a geometric method of proving the formula, since the scientists of ancient Greece did not use letters to denote numbers. They widely used not “a 2”, but “a square on a segment a”, not “ab”, but “a rectangle enclosed between segments a and b”.

In order to simplify algebraic polynomials, there are abbreviated multiplication formulas... There are not so many of them and they are easy to remember, but you need to remember them. Designations that are used in formulas can take any form (number or polynomial).

The first formula for abbreviated multiplication is called difference of squares... It consists in the fact that the square of the second number is subtracted from the square of one number, which is equal to the difference between these numbers, as well as their product.

a 2 - b 2 \u003d (a - b) (a + b)

Let's analyze for clarity:

22 2 - 4 2 = (22-4)(22+4)=18 * 26 = 468
9a 2 - 4b 2 c 2 \u003d (3a - 2bc) (3a + 2bc)

Second formula about sum of squares... It sounds like, the sum of two quantities squared is equal to the square of the first quantity, the double product of the first quantity multiplied by the second is added to it, the square of the second quantity is added to them.

(a + b) 2 \u003d a 2 + 2ab + b 2

Thanks to this formula, it becomes much easier to calculate the square of a large number, without the use of computers.

So for example: the square of 112 will be
1) First, let's analyze 112 into numbers whose squares are familiar to us
112 = 100 + 12
2) We enter the resulting in square brackets
112 2 = (100+12) 2
3) Applying the formula, we get:
112 2 = (100+12) 2 = 100 2 + 2 * 100 * 12 + 122 = 10000 + 2400+ 144 = 12544

The third formula is squared difference... Which states that the two subtracted values \u200b\u200bin the square are equal to the fact that, from the first value in the square, we subtract the double product of the first value multiplied by the second, adding the square of the second value to them.

(a + b) 2 \u003d a 2 - 2ab + b 2

where (a - b) 2 equals (b - a) 2. In proof of this, (a-b) 2 \u003d a 2 -2ab + b 2 \u003d b 2 -2ab + a 2 \u003d (b-a) 2

The fourth formula for abbreviated multiplication is called cube sum... Which sounds like: two terms of the value in a cube are equal to the cube of 1 value, the triple product of 1 value squared, multiplied by the 2nd value, is added to them the triple product of 1 value, multiplied by the square of 2, plus the second value in the cube.

(a + b) 3 \u003d a 3 + 3a 2 b + 3ab 2 + b 3

The fifth, as you already understood, is called difference cube... Which finds the differences between the quantities, as from the first designation in the cube we subtract the triple product of the first designation in the square multiplied by the second, to them is added the triple product of the first designation multiplied by the square of the second designation, minus the second designation in the cube.

(a-b) 3 \u003d a 3 - 3a 2 b + 3ab 2 - b 3

The sixth is called - sum of cubes... The sum of the cubes is equal to the product of two terms multiplied by the incomplete square of the difference, since there is no double value in the middle.

a 3 + b 3 \u003d (a + b) (a 2 -ab + b 2)

In another way, we can say the sum of cubes can be called the product in two brackets.

The seventh and final one is called difference of cubes (it can be easily confused with the difference cube formula, but these are different things). The difference between the cubes is equal to the product of the difference of two values \u200b\u200bmultiplied by the incomplete square of the sum, since there is no double value in the middle.

a 3 - b 3 \u003d (a-b) (a 2 + ab + b 2)

And so there are only 7 formulas for abbreviated multiplication, they are similar to each other and are easy to remember, the only important thing is not to get confused in the signs. They are also designed to be used in reverse order, and there are quite a few of these in the textbooks. Be careful and you will succeed.

If you have any questions about the formulas, be sure to write them in the comments. We will be glad to answer you!

If you are on maternity leave but want to make money. Just follow the link Internet business with Oriflame. Everything is written and shown in great detail there. It will be interesting!

Abbreviated Multiplication Formulas (ACF) are used for exponentiation and multiplication of numbers and expressions. Often these formulas allow you to make calculations more compact and faster.

In this article, we will list the basic formulas for abbreviated multiplication, group them in a table, consider examples of using these formulas, and also dwell on the principles of proofs of abbreviated multiplication formulas.

For the first time, the topic of FSU is considered within the framework of the "Algebra" course for the 7th grade. Below are 7 basic formulas.

Abbreviated multiplication formulas

the formula for the square of the sum: a + b 2 \u003d a 2 + 2 a b + b 2
the formula for the square of the difference: a - b 2 \u003d a 2 - 2 a b + b 2
sum cube formula: a + b 3 \u003d a 3 + 3 a 2 b + 3 a b 2 + b 3
difference cube formula: a - b 3 \u003d a 3 - 3 a 2 b + 3 a b 2 - b 3
difference of squares formula: a 2 - b 2 \u003d a - b a + b
the formula for the sum of cubes: a 3 + b 3 \u003d a + b a 2 - a b + b 2
the formula for the difference of cubes: a 3 - b 3 \u003d a - b a 2 + a b + b 2

The letters a, b, c in these expressions can be any numbers, variables or expressions. For ease of use, it is best to learn the seven basic formulas by heart. Let's summarize them in a table and present them below, encircling them with a frame.

The first four formulas allow you to calculate, respectively, the square or cube of the sum or difference of two expressions.

The fifth formula calculates the difference of the squares of the expressions by the product of their sum and the difference.

The sixth and seventh formulas are, respectively, the multiplication of the sum and the difference of the expressions by the incomplete square of the difference and the incomplete square of the sum.

The abbreviated multiplication formula is sometimes also called the abbreviated multiplication identities. This is not surprising, since every equality is an identity.

When solving practical examples, abbreviated multiplication formulas with rearranged left and right sides are often used. This is especially convenient when a factorization of a polynomial takes place.

Additional abbreviated multiplication formulas

We will not limit ourselves to the 7th grade course in algebra and add a few more formulas to our FSU table.

First, consider the Newton binomial formula.

a + b n \u003d C n 0 a n + C n 1 a n - 1 b + C n 2 a n - 2 b 2 +. ... + C n n - 1 a b n - 1 + C n n b n

Here C n k - binomial coefficients, which are in row n in the pascal triangle. Binomial coefficients are calculated by the formula:

C n k \u003d n! k! (N - k)! \u003d n (n - 1) (n - 2). ... (n - (k - 1)) k!

As you can see, the FSE for the square and the cube of the difference and the sum is a special case of the Newton binomial formula for n \u003d 2 and n \u003d 3, respectively.

But what if there are more than two terms in the sum to be raised to the power? The formula for the square of the sum of three, four or more terms will be useful.

a 1 + a 2 +. ... + a n 2 \u003d a 1 2 + a 2 2 +. ... + a n 2 + 2 a 1 a 2 + 2 a 1 a 3 +. ... + 2 a 1 a n + 2 a 2 a 3 + 2 a 2 a 4 +. ... + 2 a 2 a n + 2 a n - 1 a n

Another formula that may come in handy is the formula for the difference between the n-th powers of two terms.

a n - b n \u003d a - b a n - 1 + a n - 2 b + a n - 3 b 2 +. ... + a 2 b n - 2 + b n - 1

This formula is usually divided into two formulas - respectively for even and odd degrees.

For even indicators 2m:

a 2 m - b 2 m \u003d a 2 - b 2 a 2 m - 2 + a 2 m - 4 b 2 + a 2 m - 6 b 4 +. ... + b 2 m - 2

For odd exponents 2m + 1:

a 2 m + 1 - b 2 m + 1 \u003d a 2 - b 2 a 2 m + a 2 m - 1 b + a 2 m - 2 b 2 +. ... + b 2 m

The formulas for the difference of squares and the difference of cubes, you guessed it, are special cases of this formula for n \u003d 2 and n \u003d 3, respectively. For the difference of cubes, b is also replaced with - b.

How to read abbreviated multiplication formulas?

We will give the appropriate formulations for each formula, but first we will understand the principle of reading formulas. The most convenient way to do this is by example. Let's take the very first formula for the square of the sum of two numbers.

a + b 2 \u003d a 2 + 2 a b + b 2.

They say: the square of the sum of two expressions a and b is equal to the sum of the square of the first expression, the doubled product of the expressions and the square of the second expression.

All other formulas are read in the same way. For the square of the difference a - b 2 \u003d a 2 - 2 a b + b 2 we write:

the square of the difference between the two expressions a and b is equal to the sum of the squares of these expressions minus twice the product of the first and second expressions.

Read the formula a + b 3 \u003d a 3 + 3 a 2 b + 3 a b 2 + b 3. The cube of the sum of two expressions a and b is equal to the sum of the cubes of these expressions, three times the square of the first expression by the second and three times the square of the second expression by the first expression.

We proceed to reading the formula for the difference between cubes a - b 3 \u003d a 3 - 3 a 2 b + 3 a b 2 - b 3. The cube of the difference of two expressions a and b is equal to the cube of the first expression minus three times the square of the first expression and the second, plus three times the square of the second expression and the first expression, minus the cube of the second expression.

The fifth formula a 2 - b 2 \u003d a - b a + b (difference of squares) reads as follows: the difference of the squares of two expressions is equal to the product of the difference and the sum of the two expressions.

Expressions like a 2 + a b + b 2 and a 2 - a b + b 2 for convenience are called the incomplete square of the sum and the incomplete square of the difference, respectively.

With this in mind, the formulas for the sum and difference of the cubes read as follows:

The sum of the cubes of two expressions is equal to the product of the sum of these expressions by the incomplete square of their difference.

The difference between the cubes of two expressions is equal to the product of the difference between these expressions and the incomplete square of their sum.

FSU proof

It is quite easy to prove the FSO. Based on the properties of multiplication, we multiply the parts of the formulas in brackets.

For example, consider the formula for the square of the difference.

a - b 2 \u003d a 2 - 2 a b + b 2.

To raise an expression to the second power, you need to multiply this expression by itself.

a - b 2 \u003d a - b a - b.

Let's expand the brackets:

a - b a - b \u003d a 2 - a b - b a + b 2 \u003d a 2 - 2 a b + b 2.

The formula is proven. The rest of the FSOs are proved similarly.

Examples of FSU application

The purpose of using abbreviated multiplication formulas is to multiply and exponentiate expressions quickly and concisely. However, this is not the entire scope of the FSO. They are widely used in reducing expressions, reducing fractions, factoring polynomials. Here are some examples.

Example 1. FSO

Simplify the expression 9 y - (1 + 3 y) 2.

We apply the formula for the sum of squares and get:

9 y - (1 + 3 y) 2 \u003d 9 y - (1 + 6 y + 9 y 2) \u003d 9 y - 1 - 6 y - 9 y 2 \u003d 3 y - 1 - 9 y 2

Example 2. FSO

Reduce the fraction 8 x 3 - z 6 4 x 2 - z 4.

Note that the expression in the numerator is the difference between the cubes, and the denominator is the difference in the squares.

8 x 3 - z 6 4 x 2 - z 4 \u003d 2 x - z (4 x 2 + 2 x z + z 4) 2 x - z 2 x + z.

We shorten and get:

8 x 3 - z 6 4 x 2 - z 4 \u003d (4 x 2 + 2 x z + z 4) 2 x + z

FSOs also help to calculate the values \u200b\u200bof expressions. The main thing is to be able to notice where to apply the formula. Let's show this with an example.

Let's square the number 79. Instead of cumbersome calculations, we write:

79 = 80 - 1 ; 79 2 = 80 - 1 2 = 6400 - 160 + 1 = 6241 .

It would seem that a complex calculation was carried out quickly with just the use of the abbreviated multiplication formulas and the multiplication table.

Another important point is the selection of the square of the binomial. The expression 4 x 2 + 4 x - 3 can be converted to 2 x 2 + 2 · 2 · x · 1 + 1 2 - 4 \u003d 2 x + 1 2 - 4. Such transformations are widely used in integration.

If you notice an error in the text, please select it and press Ctrl + Enter

Multiplying a polynomial by a polynomial

! To multiply a polynomial by a polynomial, you need to multiply each term of one polynomial by each term of another polynomial and add the resulting products.

Be careful! Each term has its own sign.

Abbreviated multiplication formulas polynomials - this is, as a rule, 7 (seven) frequently occurring cases of multiplication of polynomials.

Definitions andAbbreviated multiplication formulas. Table

Table 2. Definitions of abbreviated multiplication formulas (click to enlarge)

Three abbreviated multiplication formulas for squares

1. The formula for the square of the sum.

Sum squared two expressions is equal to the square of the first expression plus twice the product of the first expression by the second plus the square of the second expression.

To better understand the formula, let's first simplify the expression (expand the formula for the square of the sum)

Now let's factorize (we will collapse the formula)

The sequence of actions for factoring:

determine which monomials were squared ( 5 and 3m);
check if the doubled product is in the middle of the formula (2 5 3m \u003d 30m);
write down the answer (5 + 3m) 2.

2. Difference square formula

Difference squared two expressions is equal to the square of the first expression minus twice the product of the first expression by the second plus the square of the second expression.

First, let's simplify the expression (expand the formula):

And then, on the contrary, let us factorize (collapse the formula):

3. Difference of squares formula

The product of the sum of two expressions by their difference is equal to the difference of the squares of these expressions.

Collapse the formula (do the multiplication)

Now let's expand the formula (factorize)

Four abbreviated multiplication formulas for cubes

4. Cube formula of the sum of two numbers

The cube of the sum of two expressions is equal to the cube of the first expression plus three times the square of the first expression and the second plus three times the square of the second plus the cube of the second expression.

The sequence of actions when "folding" the formula:

find monomials that were raised to a cube (here 4x and 1 );
check the average terms for compliance with the formula;
write down the answer.

5. Cube formula of difference of two numbers

The difference cube of the two expressions is equal to the cube of the first expression minus three times the square of the first expression and the second plus three times the first expression and the square of the second, minus the cube of the second expression.

6. The formula for the sum of cubes

The sum of the cubes of two expressions is equal to the product of the sum of the first and second expressions by the incomplete square of the difference between these expressions.

And back:

7. Cube Difference Formula

The difference between the cubes of two expressions is equal to the product of the difference between the first and second expressions by the incomplete square of the sum of these expressions.

Application of abbreviated multiplication formulas. Table

An example of using formulas in practice (oral counting).

A task: Find the area of \u200b\u200ba square with side a \u003d 71 cm.

Decision: S \u003d a 2. Using the formula for the square of the sum, we have

71 2 \u003d (70 + 1) 2 \u003d 70 2 + 2 * 70 * 1 + 1 2 \u003d 4900 + 140 + 1 \u003d 5041 cm 2

Answer: 5041 cm 2