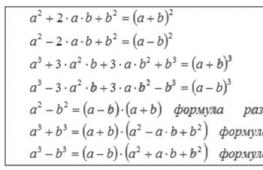Presentation on the topic "determination of dihedral angles". Segment ends Notes on problem solving

The circles are equal. Find the area of \u200b\u200bthe parallelogram. Part. Diagonal. Quadrangle. Parallelogram. Corners. Circle centers. Circle. Evidence. Triangles. Two circles. Parallelogram property. Parallelogram height. Geometry. Square. Parallelogram area. Parallelogram properties. Equality of segments. Points. Tasks. The tangent line to the circle. Sharp corner. Middle line. Parallelogram signs.

Dihedral Angle Plane - All six faces are rectangles. The distance between crossing lines. A sign of perpendicularity of two planes. Find the distance. Linear angle of a dihedral angle. Find a corner. A plane perpendicular to a straight line. Planimetry. Dihedral angles. Line a is perpendicular to the plane. The edge of a cube. Parallelepiped. Section. Planes ABC1 and A1B1D are perpendicular. Find the tangent of the angle. Diagonal.

"Consequences from the axioms of stereometry" - Section of geometry. The intersection of a straight line with a plane. Plane and straight. Planes. Build a cube image. How many faces go through one, two, three, four points. Explanation of the new material. Draw a straight line. Evidence. Decision. Oral work. Assertions. Axioms of stereometry and some of their consequences. What is stereometry. Planimetry axioms. Find the line of intersection of the planes.

"The concept of a pyramid" - Faces of a pyramid. Test questions. Lateral ribs of the pyramid. Wonders of Giza. Polyhedron. Equal angles. The pyramid in the economy. Travel route. The pyramid is based on mastaba. Side edge. Pyramids of Egypt. Pyramids in Chemistry. The base of the pyramid. Step pyramids. Model of a modern industrial enterprise. A virtual trip to the world of the pyramids. Side rib. Methane molecule structure. Adjacent side faces.

“Examples of central symmetry” - Patterns on carpets. Section. An angle with a given degree measure. Plane. A segment of a given length. Central symmetry in a six-pointed star. Central symmetry. Central symmetry in squares. Hotel "Pribaltiyskaya". Chamomile. Examples of symmetry in plants. Straight. Central symmetry in a rectangular coordinate system. Central symmetry in transport. Stereometry axioms. Central symmetry in zoology.

"Axioms of stereometry grade 10" - Axioms of stereometry. A, B, C? one straight line A, B, C? ? ? is the only plane. A plane passes through two intersecting straight lines, and, moreover, only one. Problem Given a tetrahedron MABC, each edge of which is 6 cm. Name the line along which the planes intersect: A) (MAB) and (MFC) B) (MCF) and (ABC). Consequences from the axioms of stereometry. 4. Calculate the lengths of the segments AK and AB1, if AD \u003d a. 2. Find the length of the line segment CF and the area of \u200b\u200bthe triangle ABC.

5. Circle image:

The image of a circle centered at point O1 is an ellipse centered at point O, belonging to the plane of projection α

The common perpendicular of two crossing linesis called a segment with ends on these lines, perpendicular to each of them.

Distance between crossing linesis the length of their common perpendicular. It is equal to the distance between parallel planes passing through these lines.

The angle between crossing linescalled the angle between intersecting straight lines parallel to the given intersecting straight lines.

Generalized three perpendicular theorem

Any straight line on a plane that is perpendicular to the projection that is inclined onto this plane is perpendicular and inclined.

And vice versa: if a straight line on a plane is perpendicular to an inclined one, then it is perpendicular to the projection as well.

The angle between a straight line and a planecalled the angle between a straight line and its projection on the plane (angle φ).

The angle between two intersecting planescalled the angle between the straight line of intersection of these planes with

plane perpendicular to the line of intersection of these planes (angle φ ’).

The area of \u200b\u200bthe orthogonal projection of the polygon onto the planeis equal to the product of its area by the cosine of the angle between the plane of the polygon and the projected area.

Problem 1. Through the point O of the intersection of the diagonals of the square ABCD, a perpendicular MO with a length of 15 cm is drawn to its plane. Find the distance from point M to the sides of the square if its side is 16 cm.

Answer: 17 cm.

Problem 2. Segment AS, equal to 12 cm, is perpendicular to the plane of the triangle ABC, in which AB \u003d AC \u003d 20 cm, BC \u003d 24 cm. Find the distance from point S to line BC.

Answer: 20 cm.

Problem 3. A perpendicular SD, SD \u003d 12 cm, BC \u003d 20 cm, is drawn to the plane of the rectangle ABCD, the area of \u200b\u200bwhich is 180 cm2. Find the distance from point S to the sides of the rectangle.

Answer: 12 cm, 12 cm, 15 cm, 4 34 cm.

Problem 4. The leg AC of a right-angled triangle is equal to a, angle B is equal to φ. Through the vertex of the right angle, a perpendicular MC of length a is drawn to the plane of this triangle. Find the distance from the ends of the perpendicular to the hypotenuse.

Answer: a cosϕ; a 1+ cos2 ϕ.

Problem 5. In triangle ABC, sides AB \u003d 13 cm, BC \u003d 14 cm, AC \u003d 15 cm. From the vertex A, a perpendicular AD 5 cm long is drawn to its plane. Find the distance from point D to the side BC.

Answer: 13 cm.

Problem 6. To the plane of the rhombus ABCD, in which l A \u003d 45 °, AB \u003d 8 cm, a perpendicular MC with a length of 7 cm is drawn. Find the distance from point M to the sides of the rhombus.

Answer: 7 cm, 7 cm, 9 cm, 9 cm.

Task 7. Construct common perpendiculars to lines AB and CD on the image of the cube.

Problem 8. Plane α is drawn through the AC side of the equilateral triangle ABC. The angle between the height BD of the triangle and this plane is φ. Find the angle between straight line AB and plane α.

Answer: arcsinç				sinϕ ÷.

Problem 9. Through the center O of the regular triangle ABC drawn to its plane

perpendicular MO. AB \u003d a 3. The angle between the straight line MA and the plane of the triangle is 45 °. Find the angle between the planes: 1) AMO and WMO; 2) Navy and ABC.

Answer: 1) 60 °; 2) arctan 2.

Problem 10. The planes of equilateral triangles ABC and ABD are perpendicular. Find the angle:

1) between straight line DC and plane ABC; between planes ADC and BDC.

Answer: 1) 45 °; 2) arccos 1 5.

Problem 11. Prove a theorem on the area of \u200b\u200bthe projection of a polygon for the case when the polygon is a triangle with none of its sides parallel to the projection plane.

Problem 12. The edge of the cube is equal to a. Find the cross-sectional area of \u200b\u200bthe cube by a plane passing through the top of the base at an angle of 30 ° to this base and crossing all the side edges.

Answer: 2 3 a 2.

Problem 13. The sides of the rectangle are 20 and 25 cm. Its projection onto the plane is similar to it. Find the perimeter of the projection.

Answer: 72 cm or 90 cm.

Problem 14. An isosceles triangle with a height of 16 cm was bent along the midline MN, parallel to the base of the AC, so that the vertex B is 4 cm away from the plane of the quadrilateral ACNM.

a) Find the angle between the planes AMC and MBN;

b) Construct the linear angle of the dihedral angle BMNC and find the angular measure if the orthogonal projection of the vertex B onto the plane of the quadrilateral AMNC lies outside of it;

c) Compare the angular measures of the dihedral angle BMNC and the angle BMA; d) Find the distance from point B to line AC;

e) Find the distance from the straight line MN to the plane ABC;

f) Draw a line of intersection of planes AMB and BNC.

3. Tasks for self-control

1. The edge of the cube is 10 cm. Find the distance between straight lines a and b.

2. Through the vertex A of the triangle ABC, a straight line a is drawn, perpendicular to the plane of the triangle. Find the distance between straight lines a and BC if AB \u003d 13 cm, BC \u003d 14 cm, AC \u003d 15 cm.

Answer: 12 cm.

3. The perpendicular KD is drawn to the plane of the square ABCD. The side of the square is 5 cm. Find the distance between the lines: 1) AB and KD; 2) KD and AC.

Answer: 1) 5 cm; 2) 5 2 2 cm.

4. The angle between the planes α and β is 30 °. Point A, lying in the plane α, is 12 cm from the line of intersection of the planes. Find the distance from point A to plane β.

Answer: 6 cm.

five . Through the center O of the square ABCD, the perpendicular SO is drawn to its plane. The angle between the straight line SC and the plane of the square is 60 °, AB \u003d 18 cm. Find the angle between the planes ABC and BSC.

Answer: arctg 6.

6. A square with a side of 4 2 cm bent along a straight line that passes through the midpoints of M and N sides DC and BC, so that the vertex C is removed from the plane

AMN by 1 cm.

a) find the angle between the planes ADM and CMN;

b) build the linear angle of the dihedral angle BMNC and find its angular measure if the orthogonal projection of the vertex C onto the plane of the pentagon ABNMD lies outside its boundaries;

c) compare the angular measures of the dihedral angle BMNC and the angle CNB; d) find the distance from point C to line BD;

e) find the distance from the line MN to the plane BDC;

f) draw a line of intersection of planes BNC and DMC.

Answer: a) 30 °; d) 2 × 2 + 3 cm; e) 2 - 3 cm.

7. Vertices A and D of the parallelogram ABCD lie in the plane α, and the other two - outside this plane, AB \u003d 15 cm, BC \u003d 19 cm. The projections of the parallelogram diagonals on the plane α are 20 cm and 22 cm. Find the distance from the side BC to plane α.

Directions: Use the theorem on the sum of squares of the diagonals of a parallelogram.

Answer: 12 cm.

8. Point M is removed from each side of the isosceles trapezoid at a distance of 12 cm. The bases of the trapezoid are 18 cm and 32 cm. Find the distance from point M to the plane of the trapezoid.

Answer: point M lies in the plane of the trapezoid.

9. Through vertex A of rectangle ABCD, an inclined AM is drawn to the plane of the rectangle making an angle of 50 ° with sides AD and AB. Find the angle between this oblique and the plane of the rectangle.

Answer: 32 ° 57 '.

10. The ends of the segment AB \u003d 25 cm lie on the faces of a dihedral angle equal to 60 °. From points A and B, perpendiculars AC and BD are dropped to the edge of the dihedral angle, AC \u003d 5 cm, BD \u003d 8 cm. Find CD.

Answer: 24 cm.

Lesson number 7

Topic of the lesson: "Cartesian coordinate system in space"

- to consolidate students' school knowledge of a rectangular coordinate system in space;

- systematize knowledge about the equations of figures in space;

- to consolidate the skills of solving problems for drawing up equations of geometric images in space.

1. Summary of theoretical material

t.О - origin of coordinates; Ox is the abscissa axis; Оу - ordinate axis; Оz - axis of applicate. xy, xz u yz - coordinate planes

Distance between two points

Midpoint coordinates

Shape F is given by this equation in rectangular coordinates, if a point belongs to the figure F if and only if the coordinates of this point satisfy this equation. This means that 2 conditions are met:

1) if the point belongs to the figure F, then its coordinates satisfy the equation;

2) if the numbers x, y, z satisfy this equation, then the point with such coordinates belongs to the figure F.

The equation of the sphere A sphere is the set of points in space that are distant from a given point by

given positive distance. In this case, this point is called the center of the sphere, and this distance is called its radius.

A sphere of radius R centered at point A (a; b; c) is given by the equation (by definition)

(x - a) 2 + (y - b) 2 + (z - c) 2 \u003d R 2.

If the center of the sphere coincides with the origin, then a \u003d b \u003d c \u003d 0 and the equation of the sphere is:x 2 + y 2 + z 2 \u003d R 2.

Plane equation

Theorem. A plane in space is specified in the system of rectangular coordinates x, y, z by an equation of the form Ax + By + Cz + D \u003d 0, provided that A2 + B2 + C2\u003e 0.

The converse statement is also true: the equation Ax + By + Cz + D \u003d 0 provided that A2 + B2 + C2\u003e 0 defines a plane in space in a rectangular coordinate system.

Straight line equation

A straight line in space is a line of intersection of two planes.

Р A1 x + B1 y + C1 z + D1 \u003d 0; Н о A2 x + B2 y + C2 z + D2 \u003d 0.

If the straight line AB passing through the points A (x1; y1; z1) and B (x2; y2; z2) is not parallel to any coordinate plane, then its equation has the form:

x - x1				y - y1				z - z1

2. System of tasks for classroom lessons

Problem 1. The side of the cube is 10. Find the coordinates of its vertices.

Problem 2. Find the perimeter of the triangle ABC if A (7; 1; -5), B (4; -3; -4), C (1; 3; -2).

Answer: 14 + 26.

Problem 3. Do three points A, B, C lie on the same straight line if A (3; 2; 2), B (1; 1; 1),

Answer: Yes.

Problem 4. Which of the points - A (2; 1; 5) or B (-2; 1; 6) - lie closer to the origin? Answer: Point A.

Problem 5. Points K (0; 2; 1), P (2; 0; 3) and T (-1; y; 0) are given. Find such a value for y that the condition is met: KT \u003d PT.

Answer: -3.

Problem 6. Find the coordinates of the midpoints of the sides of the triangle ABC, if A (2; 0; 2),

B (2; 2; 0), C (2; 2; 2).

Answer: A1 (2; 2; 1), B1 (2; 1; 2), C1 (2; 1; 1).

Problem 7. Find the length of the median AM of the triangle ABC, if A (2; 1; 3), B (2; 1; 5),

Answer: AM \u003d 1.

Problem 8. Which of the following equations are equations of the sphere:

a) x 2 - y 2				x 2 + y 2 + z 2 \u003d 1;	c) x 2 + y 2 + z 2 \u003d a 2;
d) x 2 + y 2		1+ x;		2x 2 + y 2 + z 2 \u003d 1;	f) x 2 + y 2 + z 2 - 2x + 3y - 4z \u003d 1?

Problem 9. Write the equations of the plane passing through: a) the Ox axis and point A (1; 1; 1);

b) points O (0; 0; 0); A (1; 2; -3) and B (2; -2; 5).

Problem 10. The plane and the sphere are given by the equations 4x + 3y – 4 \u003d 0 and x2 + y2 + z2 –2x + 8y + 8 \u003d 0. Does the center of the sphere belong to this plane?

Problem 11. Make the equation of the straight line passing through the points A (1; 3; 2) and

Find their intersection points.

Problem 13. Find the distance from the vertex D of the tetrahedron ABCD to its face ABC,

if AC \u003d CB \u003d 10, AB \u003d 12, DA \u003d 7, DB \u003d 145, DC \u003d 29.

Answer: 3.

Problem 14. Find the length of the edge AD of the tetrahedron ABCD, if AB \u003d AC \u003d BC \u003d 10,

DB \u003d 2 29, DC \u003d 46 and the distance from the vertex D to the plane of the ABC face is

Answer: 214 or 206.

3. Tasks for self-control

1. Given points K (0; 1; 1); P (2; -1; 3) and T (-1; y; 0). Find such a value for y that the condition is met: KT \u003d PT.

2. Points A (1; 2; 3) and B (3; -6; 7) are given. Find the coordinates of the midpoint of the line segment AB.

3. Find the coordinates of a point that lies on the Oy axis and is equidistant from points A (4; -1; 3) and B (1; 3; 0).

4. Find the points equidistant from points A (0; 0; 1), B (0; 1; 0), C (1; 0; 0) and at a distance of 2 from the yz plane.

five . Points A (a; 0; 0), B (0; a; 0),			С (0; 0; a) - the vertices of the triangle. Find coordinates
	the points of intersection of the medians of this triangle.
	Belongs				sphere whose equation is
	x 2 + y 2 + z 2 - 2x + 4y - 6z - 2 \u003d 0?
	Find a point	sphere crossing,		given	equation x 2 + y 2 + z 2 - 4 x \u003d 12 s

8. Make an equation for the plane parallel to the xy plane and passing through point A (2; 3; 4).

9. Points O (0; 0; 0); A (3; 0; 0); B (0; 4; 0) and O1 (0; 0; 5) - vertices of a rectangular parallelepiped. Make the equations of the planes of all its faces.

10. Make the equations of the straight line passing through the points A (1; 1; 2) andB (-3; 2; 7).

eleven . At what distance from the base of the cube is a segment of length b parallel to the base, if one end of the segment lies on the diagonal of the cube, and the other on the diagonal of the lateral face crossing with it? Cube edge length a.

Answer: (2a ± 5b 2 - a 2) ÷ 5.

12. ABCDA1 B1 C1 D1 - rectangular parallelepiped, AB \u003d BC \u003d a, AA1 \u003d 2a. Find the length of the segment MK, parallel to the face ABB1 A1, if M AD1, K DB1, AM: AD1 \u003d 2: 3.

Answer: a 3 5.

Lesson number 8

Topic of the lesson: "Vectors in space and a vector method for solving stereometric problems"

- generalize and deepen students' school knowledge about vectors, actions on them;

- continue studying the vector method for solving planimetric and stereometric problems;a for "a, b.

Property 2: (xa) × b \u003d x (a × b) for "a, b, x. Property 3: (a + b) × c \u003d a × c + b × c for" a, b, c.

Two special cases:

1) a \u003d b; a × a \u003d a2 \u003d a 2.

2) a × b \u003d 0 if and only if the vectors a and b are perpendicular. If a or b is a zero vector, then it is, by definition, perpendicular to any vector.

If a \u003d (a1; a2; a3); b \u003d (b1; b2; b3), then a × b \u003d a 1 × b 1 + a 2 × b 2 + a 3 × b 3.

Slide 2

Open lesson: "Dihedral angles" for students in grades 10-11 studying geometry according to the textbook of L.S. Atanasyan

Slide 3

Instructions for working with the presentation:

Slides are displayed with the mouse. You can start working on any slide. You can select part of the slides. You can copy the material you want.

Slide 4

Dihedral angles. 10th grade 2008

Slide 5

Lesson objectives: 1. Expand the concept: "Angle" 2. Derive the definition of dihedral angles. 3. Learn to measure dihedral angles 4. Learn to apply the properties of dihedral angles when solving problems.

Slide 6

Repetition. 1. Definition of linear angle. 2. Three perpendicular theorem. 3. Inclined and projection. 4. Definition of trigonometric functions. 4. Right triangle properties.

Slide 7

The angles are displayed gradually, at the command of the mouse, so we repeat the definition and properties Linear angle (acute, straight, obtuse) Vertical angles Adjacent angles Central angle Inscribed angle.

Slide 8

Slide 9

Perpendicular, oblique and projection. The three perpendicular theorem. Oblique and projection properties. Repeat these questions in the tasks.

Slide 10

V S A K N The perpendicular, oblique and projection are related by the Pythagorean theorem. The theorem of three perpendiculars for the straight line KS. Plane ABC KS Equal inclined ones have …… .. Large inclined ………

Slide 11

A B C D V H P N A B C D E F M H S O P R Find the angle between the line HD (AO) and the plane of the base and the side face

Slide 12

А D C B F Draw a perpendicular to DC and AD from point F ABCD - square, rhombus. How are perpendicular, oblique and oblique projection related?

Slide 13

A B C D F Where can you see the three perpendicular theorem?

Slide 14

A task.

A perpendicular BM is drawn through vertex B of square ABCD. It is known that MA \u003d 4cm MD \u003d 5cm, Find the distance from M to the plane; Distance between MV and DC. A B C D M

Slide 15

The main part of the lesson.

Practical tasks: Everyone took a file sheet, bent it into two unequal parts, made a conclusion - two intersecting half-planes with a common straight line are called a dihedral angle. How to measure it? Let's draw a common line, recall the axiom of planes, Mark a point on the edge. Draw perpendiculars to the edge from a given point in each face. We bend the edge again and conclude that the angles are different, so they need to be distinguished, how? We take scissors and make a slice-click along the perpendiculars, insert the sheet into the crack and see a linear angle. We look at the slides that give answers to the received proposals. We give the definition of measuring dihedral angles. Show the double angles on models of pyramids, prisms and on tables.

Slide 16

Dihedral angles It is known that the measure of a dihedral angle is called the measure of its linear angle. If on the edge of the dihedral angle we mark some point in each face from this point to draw rays perpendicular to the edge, then we get a linear angle. M

Slide 17

The point on the edge can be arbitrary ...

Slide 18

Definition:

α β B A C M N P

Slide 19

It is sometimes convenient to construct a linear angle of a dihedral angle in the following way: from any point A of the face α we let down to the edge a AC┴a, the perpendicular to the other face AB┴β CB will be the projection of the AC onto the plane β. Since AC┴а, BC┴ is by the converse theorem on 3 perpendiculars. ACB is the linear angle of the dihedral angle with the edge a. А В С а α β

Slide 20

Perpendicular planes. Two intersecting planes are called perpendicular if the angle between them is 90 °.

Slide 21

Properties:

If a plane passes through a straight line perpendicular to another plane, then such planes are perpendicular.

Slide 22

Solving problems:

Slide 23

Notes on solving problems.

Can be solved on computers using "Autoshapes" Can be solved on "interdosk". Can be projected directly onto a regular board or whiteboard. We display the conditions of the problem and draw and solve it right on the frame. Each student can save the solution to the problem, and the teacher will then evaluate. You can display student solutions on a common screen and consider different ways.

Slide 24

Point M is located at one of the faces of the dihedral angle equal to 30. The distance from the point to the edge of the dihedral angle is 18 cm. Calculate the distance from the projection of point M onto the second face to the edge of the dihedral angle.

Slide 25

Segments AC and BC lying in the faces of a right dihedral angle are perpendicular to its edge. Calculate the distance between points A and B if AC \u003d 10cm, BC \u003d 24cm.

Slide 26

Point K, in the face of the dihedral angle, is 12 cm away from the other face, and from the edge by Calculate the value of the dihedral angle.

Slide 27

On the edge of the dihedral angle equal to the point A. In its faces, perpendiculars to the edge AB and AC are drawn, equal to 10 cm and 8 cm, respectively. Calculate the distance between points B and C.

Slide 28

Find the distance from point D to line AB if AC \u003d CB \u003d 10, AB \u003d 16, CD \u003d 6. Draw a perpendicular from point D to line AB. Find the value of the dihedral angle at the edge AB. ▲ ABC, CD╨ABC D

Slide 29

▲ ABC, CD ╨ ABC). Find the distance from point D to straight AB, (find the value of the dihedral angle at the edge AB) ACB straight, AC \u003d 15, CB \u003d 20, SD \u003d 35. A D

Slide 30

Points M and K lie on different faces of a right dihedral angle. The distance from these points to the edge is 20 cm and 21 cm. Calculate the distance between the MK segments and the edge of the dihedral angle.

Slide 31

The ends of the segment lie in the faces of the dihedral angle and are 6 cm away from its edge. The distance between this segment and the edge is 3 cm. Calculate the value of the dihedral angle.

Slide 32

Point K is removed from each side of the equilateral triangle ABC by 8 cm, AB \u003d 24 cm.Calculate the value of the dihedral angle, the edge of which is the straight line BC, and the faces contain points K and A.

K A B C A B S

Slide 33

a) Plane M passes through side AD of square ABCD. Diagonal BD forms an angle of 45 degrees with plane M. Find the angle between the plane of the square and the plane M. b) The plane M passes through the AD side of the square ABCD and makes an angle of 30 degrees with the plane. Find the angle that makes the diagonal BD with the plane M.

Slide 34

The base of the pyramid PABCD is a rectangle ABCD, the sides of which are equal. The PAB and RBC planes are perpendicular to the ABC plane, and the PAC plane is inclined to it at an angle. Find the height and volume of the pyramid.

Slide 35

Triangular corner property.

If two plane angles are equal, then their common edge is projected onto the bisector of the third plane angle. A B C D

Slide 36

All the faces of the box are equal rhombuses, with side a and an acute angle. Find the height of the box.

Slide 37

Answer:

Slide 38

* The base of the pyramid is a rhombus. Two side faces are perpendicular to the base plane and the dihedral angle formed by them is 120 °; the other two faces are inclined to the base plane at an angle of 30 °. Pyramid height h. Find the total surface area of \u200b\u200bthe pyramid.

Slide 39

MABCD - this pyramid, ABCD - rhombus; (ABM) ┴ (ABC) and (МСВ) ┴ (ABC), means MB┴ABS). MB \u003d Н, ABC - linear angle of the dihedral angle with the edge MB, ABC \u003d 120 °. A B C D