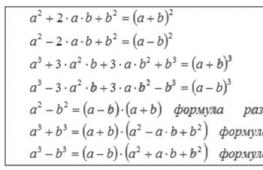All trigonometry formulas. Equation sin x \u003d a What is sin x
The task.
Find the value of x at.
Decision.
Finding the value of a function argument at which it is equal to any value means determining for which arguments the sine value will be exactly the same as specified in the condition.
In this case, we need to find out at what values \u200b\u200bthe sine value will be equal to 1/2. This can be done in several ways.
For example, use to determine at what values \u200b\u200bof x the sine function will be equal to 1/2.
Another way is to use. Let me remind you that the values \u200b\u200bof the sines lie on the Oy axis.
The most common way is to refer to, especially when it comes to such standard values \u200b\u200bfor this function as 1/2.
In all cases, do not forget about one of the most important properties of the sinus - its period.
Let's find the value 1/2 for the sine in the table and see which arguments correspond to it. The arguments of interest to us are equal to Pi / 6 and 5Pi / 6.
Let's write down all the roots that satisfy the given equation. To do this, we write down the unknown argument x we \u200b\u200bare interested in and one of the values \u200b\u200bof the argument obtained from the table, that is, Pi / 6. Let's write down for it, taking into account the sine period, all the values \u200b\u200bof the argument:
![]()
Let's take the second value and follow the same steps as in the previous case:
![]()
The complete solution to the original equation would be: ![]() and
and ![]()
q can take the value of any integer.
There are many formulas in trigonometry.
Remembering them mechanically is very difficult, almost impossible. In the classroom, many schoolchildren and students use printouts on the endpapers of textbooks and notebooks, posters on the walls, cribs, and finally. And what about the exam?
However, if you take a closer look at these formulas, you will find that they are all interconnected and have a certain symmetry. Let's analyze them, taking into account the definitions and properties of trigonometric functions, in order to determine the minimum that is really worth learning by heart.
Group I. Basic identities
sin 2 α + cos 2 α \u003d 1;
tgα \u003d ____ sinα cosα; ctgα \u003d ____ cosα sinα ;
tgα · ctgα \u003d 1;
1 + tg 2 α \u003d _____ 1 cos 2 α; 1 + ctg 2 α \u003d _____ 1 sin 2 α.
This group contains the simplest and most popular formulas. Most of the students know them. But if there are still difficulties, then in order to remember the first three formulas, mentally imagine a right-angled triangle with a hypotenuse equal to one. Then his legs will be equal, respectively, sinα by definition of sine (the ratio of the opposite leg to the hypotenuse) and cosα by the definition of cosine (the ratio of the adjacent leg to the hypotenuse).
The first formula is the Pythagorean theorem for such a triangle - the sum of the squares of the legs is equal to the square of the hypotenuse (1 2 \u003d 1), the second and third are the definitions of the tangent (the ratio of the opposite leg to the adjacent one) and the cotangent (the ratio of the adjacent leg to the opposite one).
The product of the tangent and the cotangent is 1 because the cotangent written as a fraction (formula three) is an inverted tangent (formula two). The latter consideration, by the way, allows us to exclude from the number of formulas that must be memorized, all subsequent long formulas with a cotangent. If in any difficult task you come across ctgα, just replace it with a fraction ___ 1 tgα and use the formulas for the tangent.
The last two formulas do not need to be memorized pre-symbolically. They are less common. And if required, you can always re-print them on a draft. To do this, it is enough to substitute instead of the tangent or contangent of their definitions through a fraction (formulas second and third, respectively) and bring the expression to a common denominator. But it is important to remember that such formulas that connect the squares of the tangent and cosine, and the squares of the cotangent and sine exist. Otherwise, you may not guess what transformations are needed to solve a particular problem.
Group II. Addition formulas
sin (α + β) \u003d sinα · cosβ + cosα · sinβ;
sin (α - β) \u003d sinα cosβ - cosα sinβ;
cos (α + β) \u003d cosα · cosβ - sinα · sinβ;
cos (α - β) \u003d cosα · cosβ + sinα · sinβ;
tg (α + β) \u003d tgα + tgβ _________ 1 - tgα · tgβ;
tg (α - β) \u003d
Recall the odd / even parity properties of trigonometric functions:
sin (−α) \u003d - sin (α); cos (−α) \u003d cos (α); tg (−α) \u003d - tg (α).
Of all trigonometric functions, only the cosine is an even function and does not change its sign when the argument (angle) sign changes, the rest of the functions are odd. The oddness of the function, in fact, means that the minus sign can be introduced and removed outside the function sign. Therefore, if you come across a trigonometric expression with the difference of two angles, you can always understand it as the sum of positive and negative angles.
For instance, sin ( x - 30º) \u003d sin ( x + (−30º)).
Next, we use the formula for the sum of two angles and deal with the signs:
sin ( x + (−30º)) \u003d sin x· Cos (−30º) + cos xSin (−30º) \u003d
\u003d sin x· Cos30º - cos x· Sin30º.
Thus, all formulas containing the difference in angles can simply be skipped during the first memorization. Then you should learn how to restore them in general form, first on a draft, and then mentally.
For example, tan (α - β) \u003d tan (α + (−β)) \u003d tgα + tg (−β) ___________ 1 - tgα · tg (−β) = tgα - tgβ _________ 1 + tgα · tgβ.
This will help in the future to quickly guess what transformations need to be applied to solve a particular task from trigonometry.
Sh group. Multiple Argument Formulas
sin2α \u003d 2 sinα cosα;
cos2α \u003d cos 2 α - sin 2 α;
tg2α \u003d 2tgα _______ 1 - tg 2 α;
sin3α \u003d 3sinα - 4sin 3 α;
cos3α \u003d 4cos 3 α - 3cosα.
The need to use formulas for the sine and cosine of a double angle arises very often, for the tangent it is also often. You should know these formulas by heart. Moreover, there are no difficulties in memorizing them. First, the formulas are short. Secondly, they can be easily controlled by the formulas of the previous group, based on the fact that 2α \u003d α + α.
For instance:
sin (α + β) \u003d sinα · cosβ + cosα · sinβ;
sin (α + α) \u003d sinα · cosα + cosα · sinα;
sin2α \u003d 2sinα cosα.
However, if you quickly learned these formulas, and not the previous ones, then you can do the opposite: you can remember the formula for the sum of two angles using the corresponding formula for a double angle.
For example, if you need a formula for the cosine of the sum of two angles:
1) recall the formula for the cosine of a double angle: cos2 x \u003d cos 2 x - sin 2 x;
2) we paint it long: cos ( x + x) \u003d cos xCos x - sin xSin x;
3) replace one x by α, the second by β: cos (α + β) \u003d cosα cosβ - sinα sinβ.
Practice in the same way to restore the formulas for the sine of the sum and the tangent of the sum. In critical cases, such as, for example, the USE, check the accuracy of the restored formulas using the known first quarter: 0º, 30º, 45º, 60º, 90º.
Checking the previous formula (obtained by replacing in line 3):
let be α \u003d 60 °, β \u003d 30 °, α + β \u003d 90 °,
then cos (α + β) \u003d cos90 ° \u003d 0, cosα \u003d cos60 ° \u003d 1/2, cosβ \u003d cos30 ° \u003d √3 _
/ 2, sinα \u003d sin60 ° \u003d √3 _
/ 2, sinβ \u003d sin30 ° \u003d 1/2;
we substitute the values \u200b\u200binto the formula: 0 \u003d (1/2) √3_
/2) − (√3_
/ 2) (1/2);
0 ≡ 0, no errors were found.
Formulas for a triple angle, in my opinion, do not need to be specially "crammed". They are quite rare in examinations like the USE. They are easily derived from the formulas that were above, since sin3α \u003d sin (2α + α). And for those students who, for some reason, still need to learn these formulas by heart, I advise you to pay attention to their certain "symmetry" and memorize not the formulas themselves, but the mnemonic rules. For example, the order in which the numbers are located in the two formulas "33433433", etc.
IV group. Sum / difference - into product
sinα + sinβ \u003d 2 sin α + β ____ 2Cos α - β ____ 2 ;
sinα - sinβ \u003d 2 sin α - β ____ 2Cos α + β ____ 2 ;
cosα + cosβ \u003d 2cos α + β ____ 2Cos α - β ____ 2 ;
cosα - cosβ \u003d −2 sin α - β ____ 2Sin α + β ____ 2 ;
tgα + tgβ \u003d sin (α + β) ________ cosα cosβ ;
tgα - tgβ \u003d sin (α - β) ________ cosα cosβ .
Using the odd properties of the sine and tangent functions: sin (−α) \u003d - sin (α); tg (−α) \u003d - tg (α),
it is possible to reduce the formulas for the differences of two functions to formulas for their sums. For instance,
sin90º - sin30º \u003d sin90º + sin (−30º) \u003d 2 · sin 90º + (−30º) __________ 2Cos 90º - (−30º) __________ 2 =
2 · sin30º · cos60º \u003d 2 · (1/2) · (1/2) \u003d 1/2.
Thus, the formulas for the difference between sines and tangents do not have to be learned by heart right away.
The situation is more complicated with the sum and difference of cosines. These formulas are not interchangeable. But again, using the parity of the cosine, you can remember the following rules.
The sum cosα + cosβ cannot change its sign for any change in the sign of the angles, therefore the product must also consist of even functions, i.e. two cosines.
The sign of the difference cosα - cosβ depends on the values \u200b\u200bof the functions themselves, which means that the sign of the product should depend on the ratio of the angles, therefore the product should consist of odd functions, i.e. two sinuses.
Still, this group of formulas is not the easiest to remember. This is the case when it is better to cram less, but check more. In order to avoid mistakes in the formula on the important exam, be sure to first write it down on a draft and check it in two ways. First, by substitutions β \u003d α and β \u003d −α, then by the known values \u200b\u200bof functions for prime angles. To do this, it is best to take 90º and 30º, as it was done in the example above, because the half-sum and half-difference of these values \u200b\u200bagain give simple angles, and you can easily see how equality becomes an identity for the correct option. Or, on the contrary, it is not executed if you made a mistake.
Examplechecking the formula cosα - cosβ \u003d 2 sin α - β ____ 2Sin α + β ____ 2 for the difference of cosines with a mistake !
1) Let β \u003d α, then cosα - cosα \u003d 2 sin α - α _____ 2Sin α + α _____ 2 \u003d 2sin0 sinα \u003d 0 sinα \u003d 0. cosα - cosα ≡ 0.
2) Let β \u003d - α, then cosα - cos (- α) \u003d 2 sin α - (−α) _______ 2Sin α + (−α) _______ 2 \u003d 2sinα sin0 \u003d 0 sinα \u003d 0. cosα - cos (- α) \u003d cosα - cosα ≡ 0.
These checks showed that the functions in the formula were used correctly, but due to the fact that the identity turned out to be of the form 0 ≡ 0, an error with a sign or a coefficient could be missed. We do the third check.
3) Let α \u003d 90º, β \u003d 30º, then cos90º - cos30º \u003d 2 · sin 90º - 30º ________ 2Sin 90º + 30º ________ 2 \u003d 2sin30º · sin60º \u003d 2 · (1/2) · (√3 _ /2) = √3_ /2.
cos90 - cos30 \u003d 0 - √3 _ /2 = −√3_ /2 ≠ √3_ /2.
The error was really in the sign and only in the sign before the work.
Group V. Product - Sum / Difference
sinα · sinβ \u003d 1 _ 2 (Cos (α - β) - cos (α + β));
cosα cosβ \u003d 1 _ 2 (Cos (α - β) + cos (α + β));
sinα cosβ \u003d 1 _ 2 (Sin (α - β) + sin (α + β)).
The very name of the fifth group of formulas suggests that these formulas are the reverse of the previous group. It is clear that in this case it is easier to restore the formula on a draft than to learn it again, increasing the risk of creating a "mess in your head." The only thing that makes sense to focus on for a faster recovery of the formula is the following equalities (check them):
α = α + β ____ 2 + α - β ____ 2; β = α + β ____ 2 − α - β ____ 2.
Consider example: need to convert the product sin5 xCos3 x into the sum of two trigonometric functions.
Since the product includes both sine and cosine, we take from the previous group the formula for the sum of sines, which we have already learned, and write it down on a draft.
sinα + sinβ \u003d 2 sin α + β ____ 2Cos α - β ____ 2
Let 5 x = α + β ____ 2 and 3 x = α - β ____ 2 , then α \u003d α + β ____ 2 + α - β ____ 2 = 5x + 3x = 8x, β = α + β ____ 2 − α - β ____ 2 = 5x − 3x = 2x.
We replace in the formula on the draft the values \u200b\u200bof the angles expressed in terms of the variables α and β, by the values \u200b\u200bof the angles expressed in terms of the variable x.
We get sin8 x + sin2 x \u003d 2 sin5 xCos3 x
Divide both sides of equality by 2 and write it down on the clean copy from right to left sin5 xCos3 x = 1 _ 2 (sin8 x + sin2 x). The answer is ready.
As an exercise: Explain why in the textbook there are only 3 formulas for converting the sum / difference to the product of 6, and the inverse (for converting the product to the sum or difference)?VI group. Degree reduction formulas
cos 2 α \u003d 1 + cos2α _________ 2;
sin 2 α \u003d 1 - cos2α _________ 2;
cos 3 α \u003d 3cosα + cos3α ____________ 4;
sin 3 α \u003d 3sinα - sin3α ____________ 4.
The first two formulas of this group are very necessary. They are often used when solving trigonometric equations, including the level of a unified exam, as well as when calculating integrals containing integrand functions of trigonometric type.
It may be easier to remember them in the next "one-story" form
2cos 2 α \u003d 1 + cos2α;
2 sin 2 α \u003d 1 - cos2α,
and you can always divide by 2 in your head or on a draft.
The need to use the following two formulas (with cubes of functions) in exams is much less common. In a different setting, you will always have time to use the draft. In this case, the following options are possible:
1) If you remember the last two formulas of the III group, then use them to express sin 3 α and cos 3 α by simple transformations.
2) If in the last two formulas of this group you notice elements of symmetry that contribute to their memorization, then write down the "sketches" of the formulas on the draft and check them by the values \u200b\u200bof the main angles.
3) If, in addition to the fact that such formulas for lowering the degree exist, you do not know anything about them, then solve the problem in stages, proceeding from the fact that sin 3 α \u003d sin 2 α · sinα and other learned formulas. Degree reduction formulas for a square and a product-to-sum conversion formula will be required.
VII group. Half argument
sin α _ 2 = ± √ 1 - cosα ________ 2;_____
cos α _ 2 = ± √ 1 + cosα ________ 2;_____
tg α _ 2 = ± √ 1 - cosα ________ 1 + cosα._____
I see no point in memorizing this group of formulas in the form in which they are presented in textbooks and reference books. If you understand that α is half of 2α, then this is enough to quickly deduce the required formula for the half argument, based on the first two formulas for decreasing the degree.
This also applies to the tangent of the half angle, the formula for which is obtained by dividing the sine expression by the corresponding cosine expression.
Do not forget to put the sign only when extracting the square root ± .
VIII group. Universal substitution
sinα \u003d 2tg (α / 2) _________ 1 + tg 2 (α / 2);
cosα \u003d 1 - tg 2 (α / 2) __________ 1 + tan 2 (α / 2);
tgα \u003d 2tg (α / 2) _________ 1 - tg 2 (α / 2).
These formulas can be extremely useful for solving trigonometric problems of all kinds. They allow implementing the principle of "one argument - one function", which allows you to make variable changes that reduce complex trigonometric expressions to algebraic ones. It is not for nothing that this substitution is called universal.
The first two formulas must be taught. The third can be obtained by dividing the first two by each other according to the definition of the tangent tgα \u003d sinα ___ cosα
IX group. Casting formulas.
To understand this group of trigonometric formulas, passX group. Values \u200b\u200bfor major angles.
The values \u200b\u200bof the trigonometric functions for the main angles of the first quarter are givenSo we do conclusion: Trigonometry formulas need to know. The bigger, the better. But what to spend their time and efforts on - memorizing formulas or their restoration in the process of solving problems, everyone must decide on their own.
An example of a task for using trigonometry formulas
Solve the equation sin5 xCos3 x - sin8 xCos6 x = 0.We have two different functions sin () and cos () and four! different arguments 5 x, 3x, 8x and 6 x... Without preliminary transformations, it will not work to reduce to the simplest types of trigonometric equations. Therefore, first we try to replace the products with the sums or differences of functions.
We do this in the same way as in the example above (see section).
sin (5 x + 3x) + sin (5 x − 3x) \u003d 2 sin5 xCos3 x
sin8 x + sin2 x \u003d 2 sin5 xCos3 x
sin (8 x + 6x) + sin (8 x − 6x) \u003d 2 sin8 xCos6 x
sin14 x + sin2 x \u003d 2 sin8 xCos6 x
Expressing the products from these equalities, we substitute them into the equation. We get:
(sin8 x + sin2 x) / 2 - (sin14 x + sin2 x)/2 = 0.
We multiply both sides of the equation by 2, open the brackets and give similar terms
Sin8 x + sin2 x - sin14 x - sin2 x = 0;
sin8 x - sin14 x = 0.
The equation has become much simpler, but solve it like this sin8 x \u003d sin14 x, therefore 8 x = 14x + T, where T is the period, is incorrect, since we do not know the meaning of this period. Therefore, we will use the fact that there is 0 on the right side of the equality, with which it is easy to compare the factors in any expression.
To expand sin8 x - sin14 x by factors, you need to go from difference to product. To do this, you can use the formula for the difference of sines, or again the formula for the sum of sines and oddness of the sine function (see the example in the section).
sin8 x - sin14 x \u003d sin8 x + sin (−14 x) \u003d 2 sin 8x + (−14x) __________ 2 Cos 8x − (−14x) __________ 2 \u003d sin (−3 x) Cos11 x \u003d −sin3 xCos11 x.
So the equation sin8 x - sin14 x \u003d 0 is equivalent to the equation sin3 xCos11 x \u003d 0, which, in turn, is equivalent to the combination of the two simplest equations sin3 x \u003d 0 and cos11 x \u003d 0. Solving the latter, we get two series of answers
x 1 \u003d π n/3, nϵZ
x 2 \u003d π / 22 + π k/11, kϵZ
If you find an error or typo in the text, please report it to the email address [email protected] ... I would be very grateful.
Attention, © mathematichka... Direct copying of materials on other sites is prohibited. Add links.
For solving some problems, a table of trigonometric identities will be useful, which will make it much easier to perform transformations of functions:Simplest trigonometric identities
The quotient of dividing the sine of the angle alpha by the cosine of the same angle is equal to the tangent of this angle (Formula 1). See also the proof of the correctness of the transformation of the simplest trigonometric identities.
The quotient of dividing the cosine of the alpha angle by the sine of the same angle is equal to the cotangent of the same angle (Formula 2)
The secant of an angle is equal to one divided by the cosine of the same angle (Formula 3)
The sum of the squares of the sine and cosine of the same angle is equal to one (Formula 4). see also the proof of the sum of squares of cosine and sine.
The sum of the unit and the tangent of an angle is equal to the ratio of the unit to the square of the cosine of this angle (Formula 5)
The unit plus the cotangent of the angle is equal to the quotient of dividing one by the sine square of this angle (Formula 6)
The product of the tangent and the cotangent of the same angle is equal to one (Formula 7).
Convert negative angles of trigonometric functions (even and odd)
In order to get rid of the negative value of the degree measure of the angle when calculating the sine, cosine or tangent, you can use the following trigonometric transformations (identities) based on the principles of evenness or oddness of trigonometric functions.

As seen, cosine and the secant is even function, sine, tangent and cotangent are odd functions.
The sine of a negative angle is equal to the negative sine value of that same positive angle (minus sine alpha).
The cosine "minus alpha" will give the same value as the cosine of the angle alpha.
Tangent minus alpha is equal to minus tangent alpha.
Double angle reduction formulas (sine, cosine, tangent and cotangent of double angle)
If you need to divide an angle in half, or vice versa, go from a double angle to a single angle, you can use the following trigonometric identities:

Double angle conversion (sine of double angle, cosine of double angle and tangent of double angle) to single occurs according to the following rules:
Double angle sine is equal to twice the product of sine and cosine of a single angle
Double angle cosine is equal to the difference between the square of the cosine of a single angle and the square of the sine of this angle
Double angle cosine equal to twice the square of the cosine of a single angle minus one
Double angle cosine equal to one minus double sine square of a single angle
Double angle tangent is equal to a fraction, the numerator of which is the double tangent of a single angle, and the denominator is equal to one minus the tangent of the square of a single angle.
Double angle cotangent is equal to a fraction, the numerator of which is the square of the cotangent of a single angle minus one, and the denominator is equal to twice the cotangent of a single angle
Universal trigonometric substitution formulas
The transformation formulas below can be useful when you need to divide the argument of a trigonometric function (sin α, cos α, tan α) by two and reduce the expression to the value of half the angle. From the value of α we obtain α / 2.These formulas are called formulas of universal trigonometric substitution... Their value lies in the fact that the trigonometric expression with their help is reduced to the expression of the tangent of half an angle, regardless of what trigonometric functions (sin cos tg ctg) were in the expression initially. After that, the equation with the tangent of half the angle is much easier to solve.
Trigonometric transformations of half an angle
The following are the formulas for the trigonometric conversion of half an angle to an integer value.The value of the argument of the trigonometric function α / 2 is reduced to the value of the argument of the trigonometric function α.
Trigonometric formulas for adding angles

cos (α - β) \u003d cos α cos β + sin α sin β
sin (α + β) \u003d sin α cos β + sin β cos α
sin (α - β) \u003d sin α cos β - sin β cos α
cos (α + β) \u003d cos α cos β - sin α sin β
Tangent and cotangent of the sum of anglesalpha and beta can be converted according to the following trigonometric function conversion rules:
Tangent of the sum of angles is equal to the fraction, the numerator of which is the sum of the tangent of the first and the tangent of the second angle, and the denominator is one minus the product of the tangent of the first angle and the tangent of the second angle.
Angle difference tangent is equal to a fraction, the numerator of which is equal to the difference between the tangent of the angle to be reduced and the tangent of the angle to be subtracted, and the denominator is equal to one plus the product of the tangents of these angles.
Cotangent of the sum of angles is equal to a fraction, the numerator of which is equal to the product of the cotangents of these angles plus one, and the denominator is equal to the difference between the cotangent of the second angle and the cotangent of the first angle.
Angle difference cotangent is equal to the fraction, the numerator of which is the product of the cotangents of these angles minus one, and the denominator is equal to the sum of the cotangents of these angles.
These trigonometric identities are convenient to use when you need to calculate, for example, the tangent of 105 degrees (tg 105). If you represent it as tg (45 + 60), then you can use the given identical transformations of the tangent of the sum of angles, after which you simply substitute the tabular values \u200b\u200bof the tangent 45 and the tangent 60 degrees.
Sum or Difference Conversion Formulas for Trigonometric Functions
Expressions representing the sum of the form sin α + sin β can be transformed using the following formulas:
Triple angle formulas - convert sin3α cos3α tg3α to sinα cosα tgα
Sometimes it is necessary to transform the triple value of the angle so that the angle α becomes the argument of the trigonometric function instead of 3α.In this case, you can use the formulas (identities) for transforming the triple angle:

Transformation formulas for the product of trigonometric functions
If it becomes necessary to transform the product of sines of different angles of cosines of different angles, or even the product of sine and cosine, then you can use the following trigonometric identities:
In this case, the product of the sine, cosine or tangent functions of different angles will be converted to the sum or difference.
Trigonometric function reduction formulas
You need to use the cast table as follows. In the line, select the function that interests us. The column contains the corner. For example, the sine of the angle (α + 90) at the intersection of the first row and the first column, we find out that sin (α + 90) \u003d cos α.
In trigonometry, many formulas are easier to deduce than memorize. The cosine of a double angle is a wonderful formula! It allows you to derive degree reduction and half angle formulas.
So, we need the cosine of the double angle and the trigonometric unit:
They are even similar: in the double angle cosine formula, the difference between the squares of the cosine and sine, and in the trigonometric unit, their sum. If we express the cosine from the trigonometric unit:
and substitute it in the cosine of the double angle, we get:
This is another double angle cosine formula:
This formula is the key to obtaining the degree reduction formula:
So, the formula for lowering the degree of sine:
![]()
If in it the angle alpha is replaced by a half angle alpha in half, and the double angle two alphas are replaced by an angle alpha, then we get the formula for the half angle for the sine:
![]()
Now we express the sine from the trigonometric unit:
Substitute this expression into the double angle cosine formula:
![]()
We got another formula for the cosine of a double angle:
This formula is the key to finding the cosine degree and half angle reduction formula for the cosine.
Thus, the formula for lowering the degree of the cosine is:
![]()
If in it we replace α by α / 2, and 2α - by α, then we obtain the formula for the half argument for the cosine:
![]()
Since the tangent is the ratio of sine to cosine, the formula for the tangent is:
![]()
Cotangent is the ratio of cosine to sine. Therefore, the formula for the cotangent is:
![]()
Of course, in the process of simplifying trigonometric expressions, half-angle formulas or lowering the degree does not make sense to deduce each time. It is much easier to put a leaflet with formulas in front of you. And the simplification will advance faster, and the visual memory will be included in memorization.
But it is still worth deriving these formulas several times. Then you will be absolutely sure that on the exam, when there is no way to use the cheat sheet, you can easily get them if the need arises.
Sine values \u200b\u200bare enclosed in the interval [-1; 1], ie -1 ≤ sin α ≤ 1. Therefore, if | a | \u003e 1, then the equation sin x \u003d a has no roots. For example, the equation sin x \u003d 2 has no roots.
Let's turn to some tasks.
Solve the equation sin x \u003d 1/2.
Decision.
Note that sin x is the ordinate of the unit circle point, which is obtained by rotating the point P (1; 0) by an angle x around the origin.
The ordinate equal to ½ is present at two points of the circle M 1 and M 2.
Since 1/2 \u003d sin π / 6, the point M 1 is obtained from the point P (1; 0) by turning through an angle x 1 \u003d π / 6, and also by angles x \u003d π / 6 + 2πk, where k \u003d +/- 1, +/- 2, ...
Point М 2 is obtained from point Р (1; 0) as a result of rotation through the angle х 2 \u003d 5π / 6, as well as through angles х \u003d 5π / 6 + 2πk, where k \u003d +/- 1, +/- 2, ... , i.e. at the angles х \u003d π - π / 6 + 2πk, where k \u003d +/- 1, +/- 2,….
So, all the roots of the equation sin x \u003d 1/2 can be found by the formulas x \u003d π / 6 + 2πk, x \u003d π - π / 6 + 2πk, where k € Z.
These formulas can be combined into one: x \u003d (-1) n π / 6 + πn, where n € Z (1).
Indeed, if n is an even number, i.e. n \u003d 2k, then from formula (1) we obtain х \u003d π / 6 + 2πk, and if n is an odd number, i.e. n \u003d 2k + 1, then from formula (1) we obtain х \u003d π - π / 6 + 2πk.
Answer. х \u003d (-1) n π / 6 + πn, where n € Z.
Solve the equation sin x \u003d -1/2.
Decision.
The ordinate -1/2 has two points of the unit circle M 1 and M 2, where x 1 \u003d -π / 6, x 2 \u003d -5π / 6. Therefore, all the roots of the equation sin x \u003d -1/2 can be found by the formulas x \u003d -π / 6 + 2πk, x \u003d -5π / 6 + 2πk, k € Z.
We can combine these formulas into one: x \u003d (-1) n (-π / 6) + πn, n € Z (2).
Indeed, if n \u003d 2k, then by formula (2) we obtain x \u003d -π / 6 + 2πk, and if n \u003d 2k - 1, then by formula (2) we find x \u003d -5π / 6 + 2πk.
Answer. x \u003d (-1) n (-π / 6) + πn, n € Z.
Thus, each of the equations sin x \u003d 1/2 and sin x \u003d -1/2 has an infinite number of roots.
On the interval -π / 2 ≤ x ≤ π / 2, each of these equations has only one root:
x 1 \u003d π / 6 is the root of the equation sin x \u003d 1/2 and x 1 \u003d -π / 6 is the root of the equation sin x \u003d -1/2.
The number π / 6 is called the arcsine of the number 1/2 and is written: arcsin 1/2 \u003d π / 6; the number -π / 6 is called the arcsine of the number -1/2 and is written: arcsin (-1/2) \u003d -π / 6.
In general, the equation sin x \u003d a, where -1 ≤ a ≤ 1, has only one root on the interval -π / 2 ≤ x ≤ π / 2. If a ≥ 0, then the root is in the interval; if a< 0, то в промежутке [-π/2; 0). Этот корень называют арксинусом числа а и обозначают arcsin а.
Thus, the arcsine of the number a € [–1; 1] such a number is called a € [–π / 2; π / 2], whose sine is equal to a.
arcsin а \u003d α, if sin α \u003d а and -π / 2 ≤ х ≤ π / 2 (3).
For example, arcsin √2 / 2 \u003d π / 4, since sin π / 4 \u003d √2 / 2 and - π / 2 ≤ π / 4 ≤ π / 2;
arcsin (-√3 / 2) \u003d -π / 3, since sin (-π / 3) \u003d -√3 / 2 and - π / 2 ≤  - π / 3 ≤ π / 2.
- π / 3 ≤ π / 2.
Similarly to how it was done in solving problems 1 and 2, it can be shown that the roots of the equation sin x \u003d a, where | a | ≤ 1, are expressed by the formula
х \u003d (-1) n аrcsin а + πn, n € Z (4).
We can also prove that for any a € [-1; 1] the formula arcsin (-a) \u003d -arcsin a is valid.
From formula (4) it follows that the roots of the equation
sin x \u003d a for a \u003d 0, a \u003d 1, a \u003d -1 can be found using simpler formulas:
sin х \u003d 0 х \u003d πn, n € Z (5)
sin x \u003d 1 x \u003d π / 2 + 2πn, n € Z (6)
sin x \u003d -1 x \u003d -π / 2 + 2πn, n € Z (7)
site, with full or partial copying of the material, a link to the source is required.